2.3. Decoding on simulated data¶
Objectives
- Understand linear estimators (SVM, elastic net, ridge)
- Use the scikit-learn’s linear models
2.3.1. Simple NeuroImaging-like simulations¶
We simulate data as in Michel et al. 2012 : a linear model with a random design matrix X:
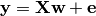
- w: the weights of the linear model correspond to the predictive brain regions. Here, in the simulations, they form a 3D image with 5, four of which in opposite corners and one in the middle.
- X: the design matrix corresponds to the observed fMRI data. Here we simulate random normal variables and smooth them as in Gaussian fields.
- e is random normal noise.
We provide a black-box function to create the data in the example script.
2.3.2. Running various estimators¶
We can now run different estimators and look at their prediction score, as well as the feature maps that they recover. Namely, we will use
- A support vector regression (SVM)
- An elastic-net
- A Bayesian ridge estimator, i.e. a ridge estimator that sets its parameter according to a metaprior
- A ridge estimator that set its parameter by cross-validation
Note that the RidgeCV and the ElasticNetCV have names ending in CV that stands for cross-validation: in the list of possible alpha values that they are given, they choose the best by cross-validation.
As the estimators expose a fairly consistent API, we can all fit them in a for loop: they all have a fit method for fitting the data, a score method to retrieve the prediction score, and because they are all linear models, a coef_ attribute that stores the coefficients w estimated (see the code of the simulation).
Note
All parameters estimated from the data end with an underscore
Exercise
Use recursive feature elimination (RFE) with the SVM:
>>> from sklearn.feature_selection import RFE
Read the object’s documentation to find out how to use RFE.
Performance tip: increase the step parameter, or it will be very slow.
Source code to run the simulation
The full file to run the simulation can be found in example_decoding_plot_simulated_data.py





